

All you need to know is the Voronoi object vor contains all of the Voronoi information (regions, ridges, vertices, etc.) for plotting diagrams.
Simple_voronoi(vor, saveas="square", lim=(-0.25,1.25))Ĭonveniently, scipy.spatial utilizes an optimized computational geometry library to compute Voronoi tessellations, so we won’t have to worry about those details. Square = ĭef simple_voronoi(vor, saveas=None, lim=None):įig = voronoi_plot_2d(vor, show_points=True, show_vertices=True, s=4) from scipy.spatial import Voronoi, voronoi_plot_2d
SCIPY SPATIAL CODE
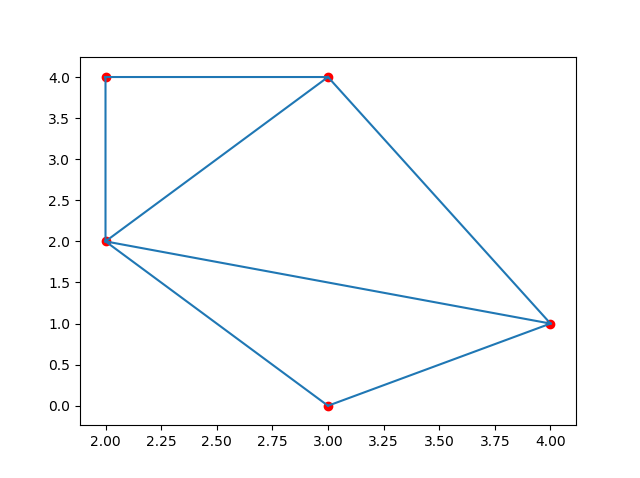
Since all of the cells are on the edge with no possible intersections, there are no finite polygons.īefore we add one more point to the square to get a finite region, let’s show the Python code to generate these simple diagrams. within a square), or it is equally distant to at least two corners (i.e. As for an interpretation, this diagram labels all of 2D space into two categories: any point on the plane is either closest to one of four corners in the unit square (i.e. Seeds are colored as blue dots at the corners of the unit square, dotted lines represent edges of an infinite polygon, and orange dots are Voronoi vertices. Each corner will be a seed, so there will be four Voronoi cells.
SCIPY SPATIAL HOW TO
To illustrate what Voronoi diagrams are and how to make them, let’s start with a very simple dataset: the four corners of the unit square. This extension occurs because regions are defined as all points nearest to a single seed and not the others so, since 2D space has infinite coordinates, there will always be infinite regions.
SCIPY SPATIAL GENERATOR
Importantly, note that if the region’s generator is on the edge of the seed space and has no possible intersections, it will extend to infinity.
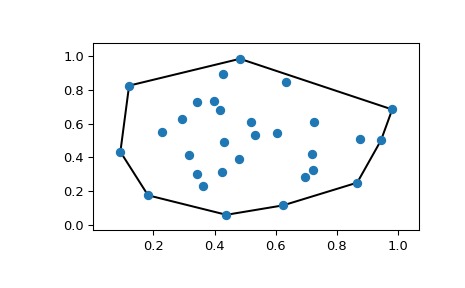
The Voronoi Diagram is the concatenation of n regions generated by the seeds. It’s important to recall that a generator, D k, comes from the input data, whereas points in its region, R k, is the output. In English, the equation is “This region is equal to the set of points in 2D space such that the distance between any one of these points and this generator is less than the distance between the point and all other generators.” To fully understand the math, be sure to map the words to every symbol in the equation. For each seed k in D, a region R k is defined by the Region equation. Given a distance metric dist and a dataset D of n 2-dimensional generator coordinates, a Voronoi diagram partitions the plane into n distinct regions.


 0 kommentar(er)
0 kommentar(er)
